In this follow up post we apply the same methods we developed previously to a different dataset. In this third post we mix the previous two datasets.
So, on the one hand, we have noise signals, on the other hand we have innovators and followers.
Again, as previously, we make use of the github hosted package timeseries_utils, and a script, which follows here:
# load data
import os
os.chdir('** use your own dictionary, where you want to save your plots **')
import numpy as np
import matplotlib.pyplot as plt
from timeseries_utils import Configuration, Data
from timeseries_utils import calculateForecastSkillScore
# configuration
C = Configuration()
C.dictionary['nOfPoints'] = 600
# below 300 things dont work so nicely, so we use a value considerably above that
C.dictionary['inSampleRatio'] = 0.5
C.dictionary['differencingOrder'] = 1
C.dictionary['p_order'] = 7
C.dictionary['steps_prediction'] = 1
C.dictionary['epochs'] = 100
C.dictionary['verbose'] = 0
C.dictionary['modelname'] = modelname
# create data
# # set random seed for reproducibility
np.random.seed(178)
D = Data()
nOfSeries = 7
artificial_x, artificial_SERIES = artificial_data(nOfPoints = C.dictionary['nOfPoints'],
nOfSeries = nOfSeries,
f_rauschFactor = 0.5)
D.setInnovator('innovator1', C=C)
D.setFollower(name = 'follower1', otherSeriesName='innovator1', shiftBy=-1)
w1 = 0.5
w2 = 1 - w1
f3 = w1 * D.dictionaryTimeseries['innovator1'] + w2 * artificial_SERIES[:,3]
f4 = D.dictionaryTimeseries['innovator1'] * artificial_SERIES[:,3]
f5 = np.cos(D.dictionaryTimeseries['innovator1']) * np.sin(artificial_SERIES[:,3])
D.setFollower('mixture1',
otherSeriesName='innovator1 + a signal',
otherSeries=f3,
shiftBy=-1)
D.setFollower('mixture2',
otherSeriesName='innovator1 * a signal',
otherSeries=f4,
shiftBy=-1)
D.setFollower('mixture3',
otherSeriesName='cos(innovator1) * sin(a signal)',
otherSeries=f5,
shiftBy=-1)
SERIES_train = D.train(D.SERIES(), Configuration=C)
SERIES_test = D.test(D.SERIES(), Configuration=C)
VARIABLES_train = D.train(D.VARIABLES(), Configuration=C)
VARIABLES_test = D.test(D.VARIABLES(), Configuration=C)
#define, fit model; predict with with model
Prediction, Model = defineFitPredict(C=C,
D=D,
VARIABLES_train=VARIABLES_train,
SERIES_train=SERIES_train,
VARIABLES_test=VARIABLES_test,
SERIES_test=SERIES_test)
# calculate Accuracy : 0% as good as NULL-Hypothesis, 100% is perfect prediction
Skill = calculateForecastSkillScore(actual=SERIES_test, predicted=Prediction, movingAverage=20)
f, axarr = plt.subplots(1, 2, sharey=False)
f.suptitle(predictionModel)
axarr[0].plot(SERIES_test)
axarr[0].plot(Prediction)
axarr[0].set_title('Series, Prediction vs Time')
axarr[0].set_xlabel('Time')
axarr[0].set_ylabel('Series, Prediction')
axarr[1].plot(SERIES_test, Prediction, '.')
axarr[1].set_title('Prediction vs Series')
axarr[1].set_xlabel('Series')
axarr[1].set_ylabel('Prediction')
plt.savefig('pictures/' + plotname + '_1.png', dpi=300)
plt.show()
f, axarr = plt.subplots(1, D.numberOfSeries(), sharey=True)
f.suptitle(predictionModel + ', Prediction vs Series')
seriesTitles = list(D.dictionaryTimeseries.keys())
for plotNumber in range(D.numberOfSeries()):
seriesNumber = plotNumber
axarr[plotNumber].plot(SERIES_test[:,seriesNumber], Prediction[:,seriesNumber], '.')
# axarr[plotNumber].plot(SERIES_test[:-x,seriesNumber], Prediction[x:,seriesNumber], '.')
if Skill[seriesNumber] < 50:
axarr[plotNumber].set_title('S. ' + str(Skill[seriesNumber]) + '%', color='red')
if Skill[seriesNumber] > 50:
axarr[plotNumber].set_title('S. ' + str(Skill[seriesNumber]) + '%', color='green', fontweight='bold')
axarr[plotNumber].set_xlabel(seriesTitles[seriesNumber])
axarr[plotNumber].set_ylabel('Prediction')
axarr[plotNumber].set_xticklabels([])
plt.savefig('pictures/' + plotname + '_2.png', dpi=300)
plt.show()
# end: # second set of plots
Data
As stated, the main difference to the previous posts is the data.
In this post the data is composed of an innovator, a follower and some mixtures.
Arima
As mentioned, the defineFitPredict needs to be defined for each forecasting technique. In the case of arima we use defineFitPredict_ARIMA, which is supplied by our package timeseries_utils.
from timeseries_utils import artificial_data from timeseries_utils import defineFitPredict_ARIMA, defineFitPredict_DENSE, defineFitPredict_LSTM defineFitPredict = defineFitPredict_ARIMA predictionModel = 'Arima'
Now we run the script shown above.
The configuration is this:
The configuration is (in alphabetical order):
differencingOrder:1
epochs:100
inSampleRatio:0.5
...
nOfPoints:600
p_order:7
splitPoint:300
steps_prediction:1
verbose:0
The data summary is:
SERIES-shape:(600, 5)
follower1:{'shiftedBy': -1, 'follows': 'innovator1'}
innovator1:{'nOfPoints': 600}
mixture1:{'shiftedBy': -1, 'follows': 'innovator1 + a signal'}
mixture2:{'shiftedBy': -1, 'follows': 'innovator1 * a signal'}
mixture3:{'shiftedBy': -1, 'follows': 'cos(innovator1) * sin(a signal)'}
The result is:
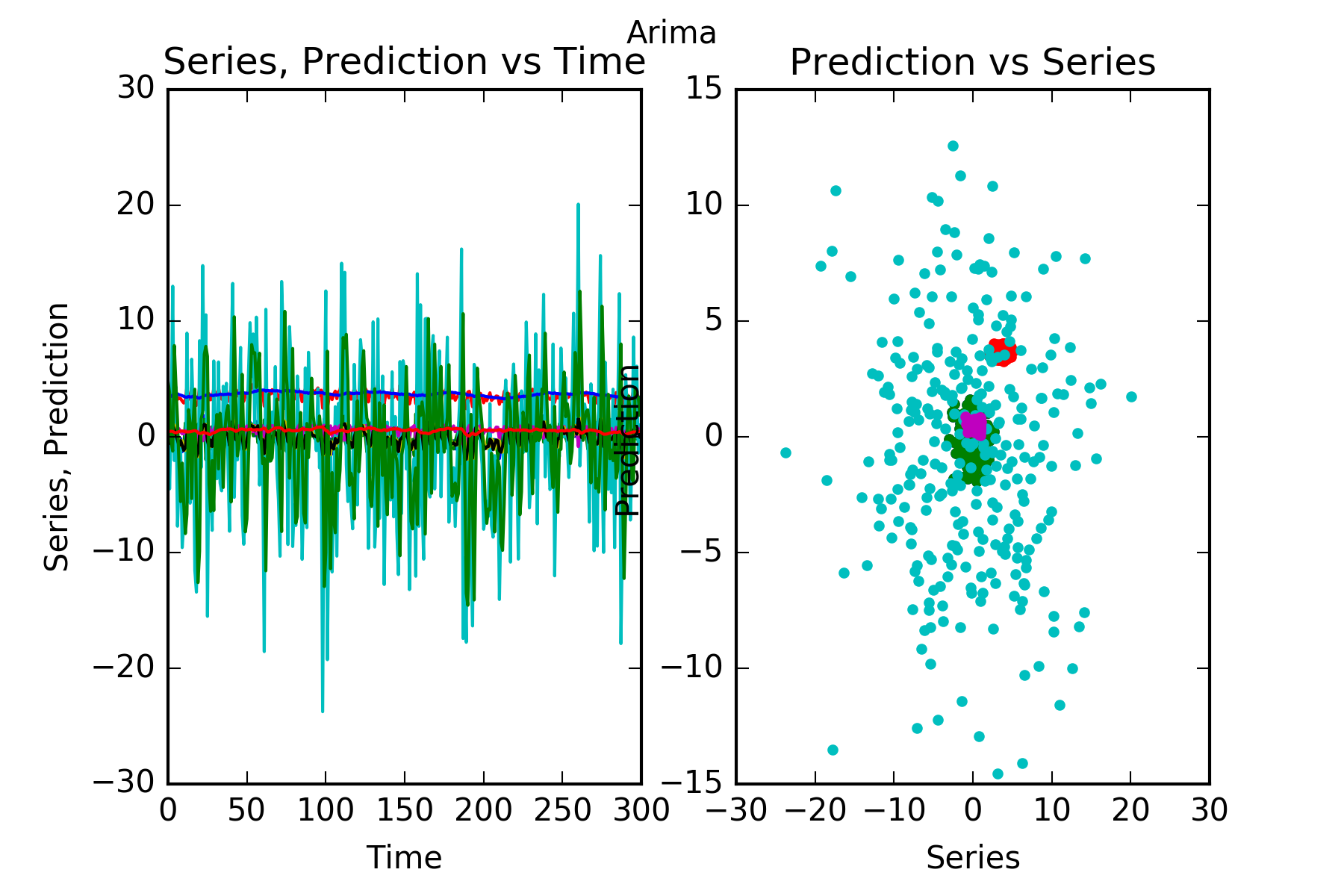
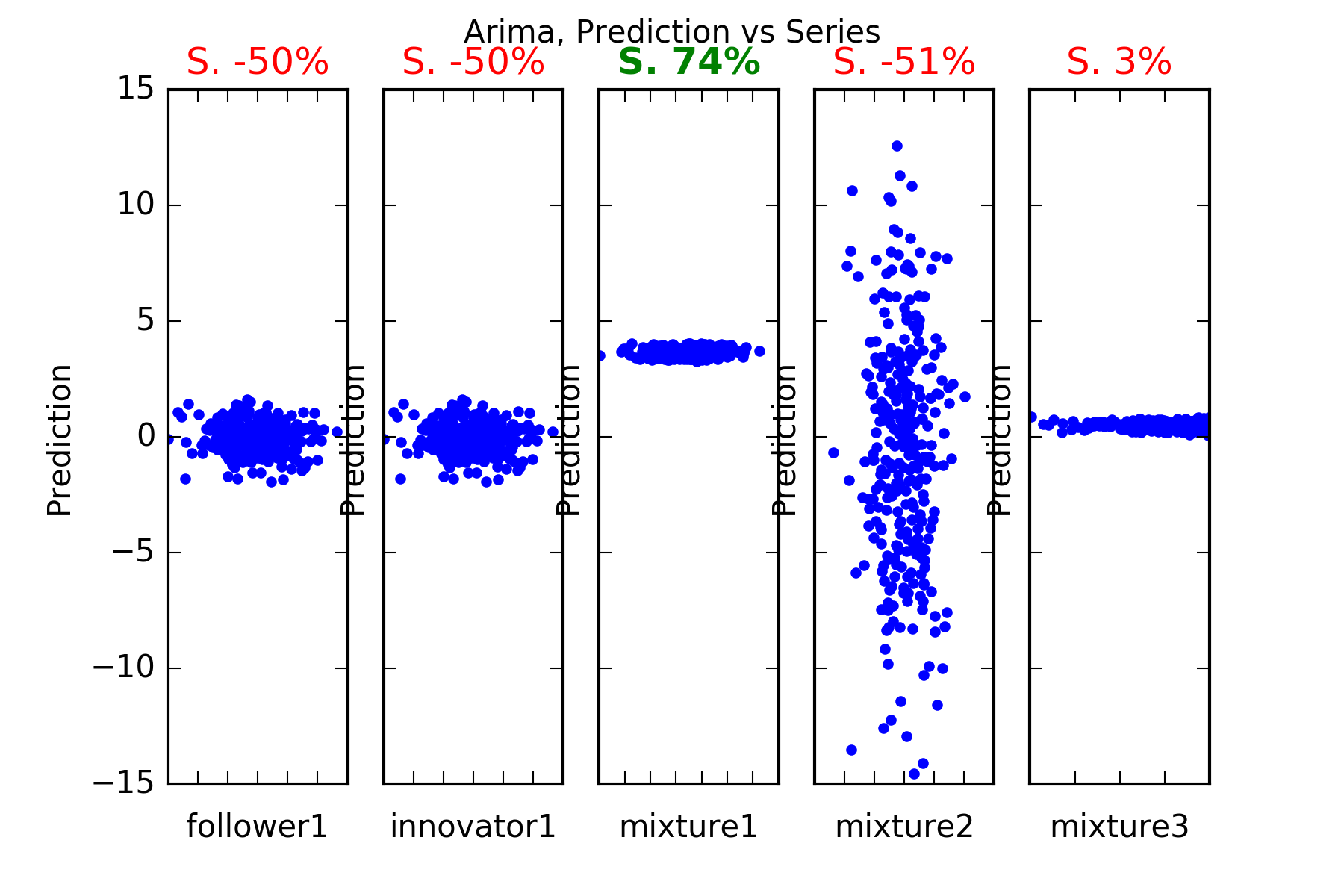
Interpretation : As is evident in the figures and the reported skill scores arima struggles to predict anything meaningful at all, except for mixture1, which contains a signal. The more complicated signal-bearing mixtures muixture2 and mixture3 are not predicted any better than by the benchmark.
Dense
As mentioned, the defineFitPredict needs to be defined for each forecasting technique. In the case of our dense network we usedefineFitPredict_DENSE, which is also supplied by our package timeseries_utils.
from timeseries_utils import artificial_data from timeseries_utils import defineFitPredict_ARIMA, defineFitPredict_DENSE, defineFitPredict_LSTM defineFitPredict = defineFitPredict_DENSE predictionModel = 'Dense' modelname = predictionModel + '-mixture' plotname = 'forecasting_3_dense'
Now we run the script shown above.
The model summary is this:
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= flatten_1 (Flatten) (None, 35) 0 _________________________________________________________________ dense_1 (Dense) (None, 32) 1152 _________________________________________________________________ dropout_1 (Dropout) (None, 32) 0 _________________________________________________________________ dense_2 (Dense) (None, 5) 165 ================================================================= Total params: 1,317 Trainable params: 1,317 Non-trainable params: 0 _________________________________________________________________
The result is:
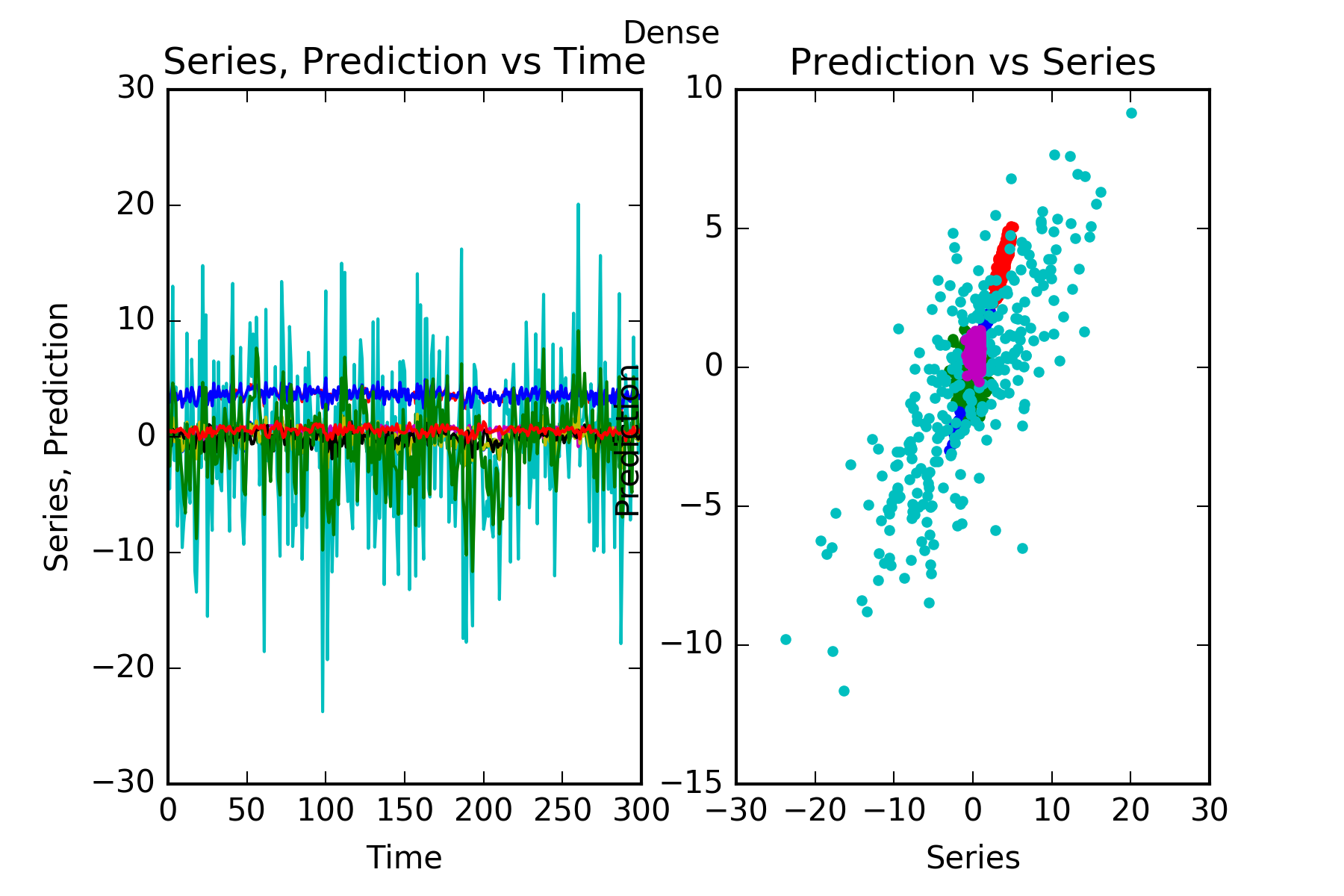
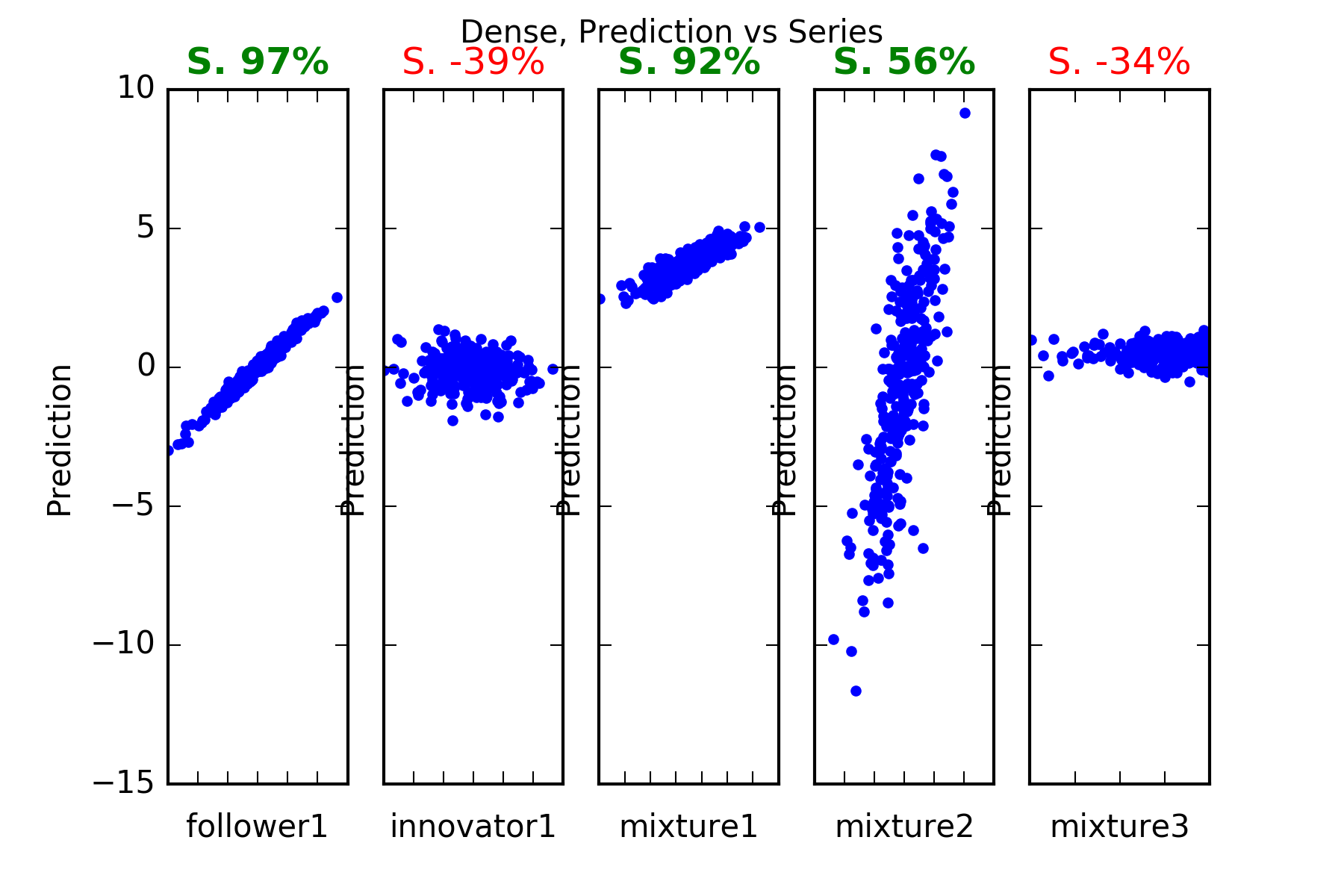
Interpretation : Dense does a pretty good job. Of course it cannot predict the innovator1, however it noticeably fails with the complicated construction of mixture3.
LSTM
As mentioned, the defineFitPredict needs to be defined for each forecasting technique. In the case of our LSTM network we use defineFitPredict_LSTM, which is also supplied by our package timeseries_utils.
from timeseries_utils import artificial_data from timeseries_utils import defineFitPredict_ARIMA, defineFitPredict_DENSE, defineFitPredict_LSTM defineFitPredict = defineFitPredict_LSTM predictionModel = 'LSTM'
Now we run the script shown above.
The model summary is this:
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= lstm_1 (LSTM) (None, 16) 1408 _________________________________________________________________ dense_1 (Dense) (None, 5) 85 ================================================================= Total params: 1,493 Trainable params: 1,493 Non-trainable params: 0 _________________________________________________________________
The result is:
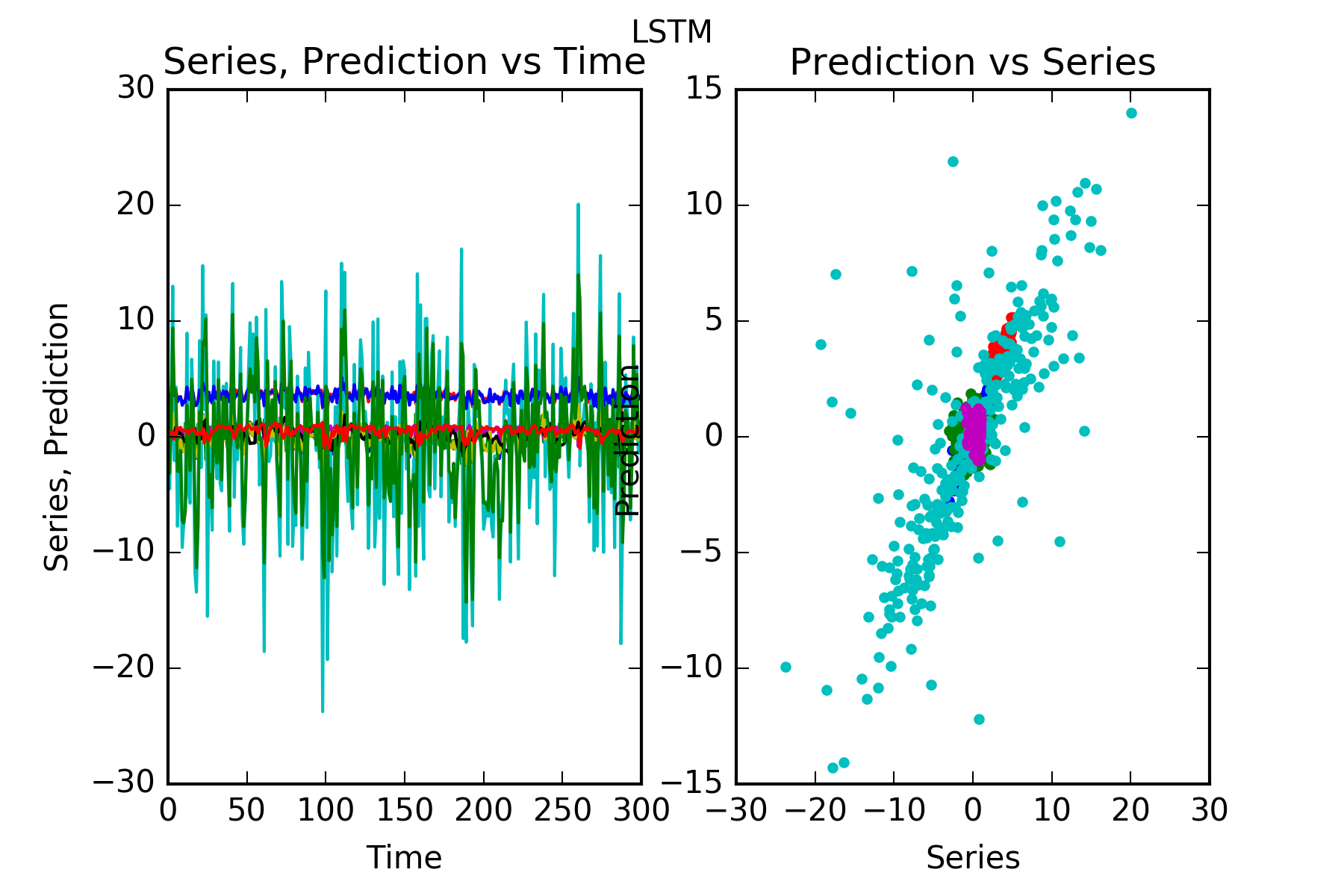
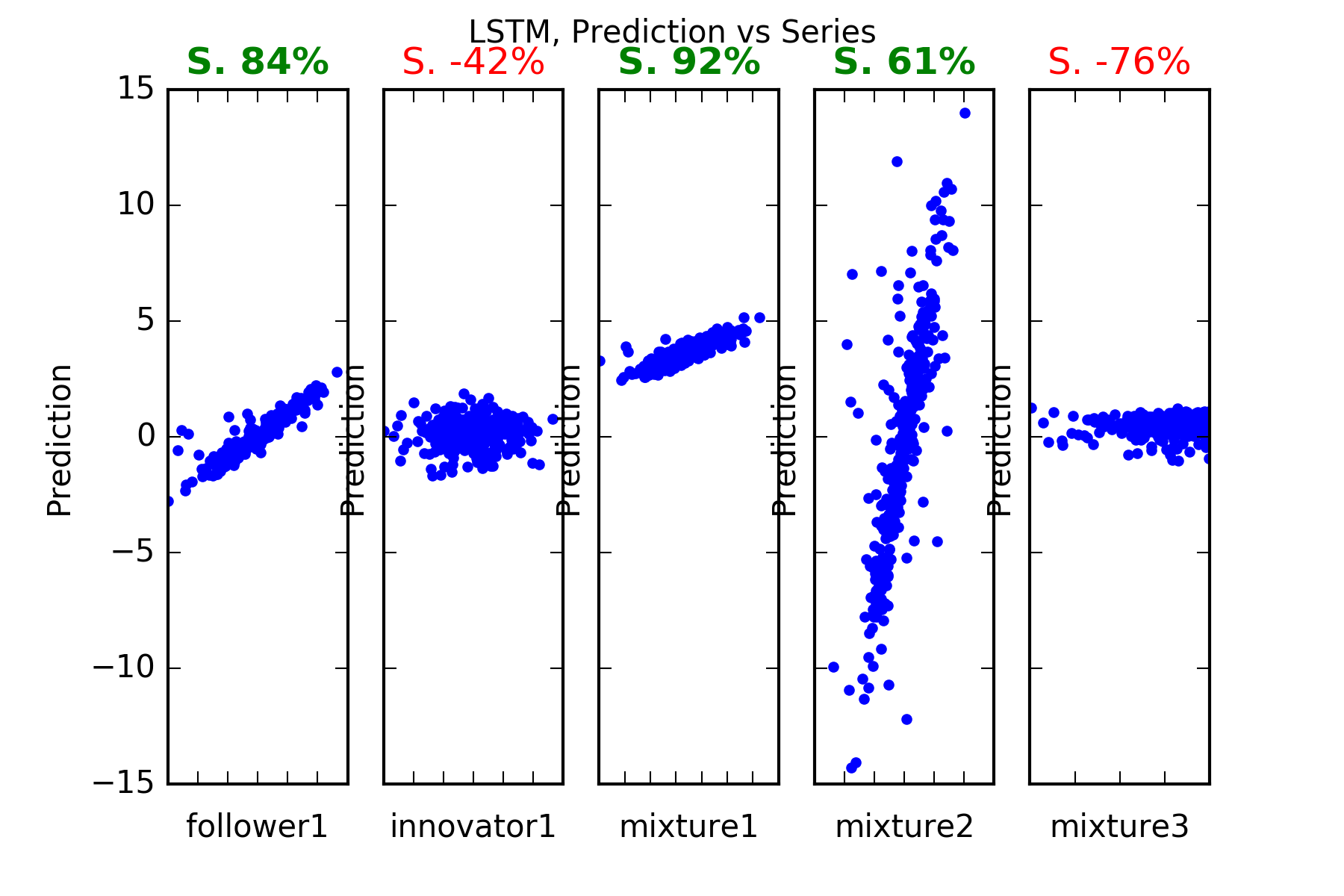
Interpretation : LSTM does a pretty good job. Of course it cannot predict the innovator1, in particular it noticeably fails with the complicated construction of mixture3.
| Method/Timeseries | Arima | Dense | LSTM |
|---|---|---|---|
| follower1 | ✕ | ✔ | ✔ |
| innovator1 | ✕ | ✕ | ✕ |
| mixture1 | ✔ | ✔ | ✔ |
| mixture2 | ✕ | ✔ | ✔ |
| mixture3 | ✕ | ✕ | ✕ |
The joint winners are Dense and LSTM.
