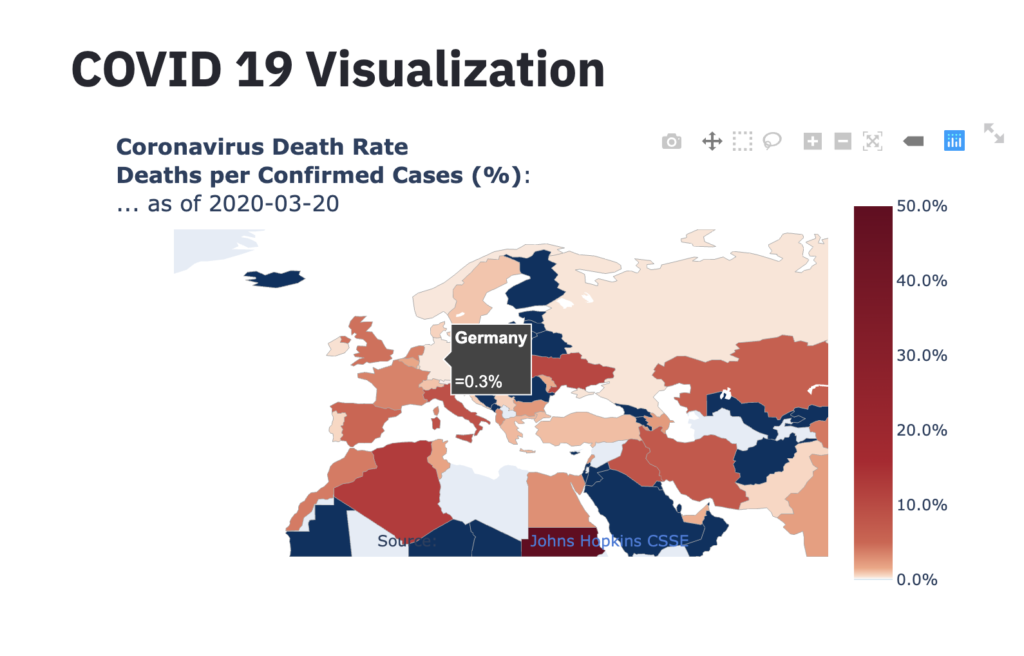
New technology stack for financial-timeseries-dashboard
I have updated my previous implementation of the financial-timeseries-dashboard in three aspects: The code is available at : https://github.com/hfwittmann/financial-timeseries-dashboard/tree/kedro-based The dashboard is available at https://dax.arthought.com/, the fast-api rest-api is available at https://dax-backend.arthought.com Kedro is a workflow management tool for data pipelines. It provides a standardized project structure and tools for building, …